Озадачился подбором профилей на трапециевидное крыло и уперся в товарища Рейнольдса. Он понапридумывал разных многоэтажных чисел, с которыми теперь приходится разбираться ;D
Если я правильно понимаю суть вопроса, то для любого тела с любыми размерами, двигающегося в любой среде кроме вакуума, существуют эти самые числа. Они меняются в зависимости от собственно этой среды, её вязкости. И еще определяющими является скорость движения и размер тела. Для воздуха, если сильно высоко не забираться есть простая формула Re=70*V*L.
Где L - к примеру хорда крыла, в миллиметрах; V - соответственно скорость в м/с. А само число вообще безразмерное.
Т.е. если модель с хордой 100 мм летит со скоростью порядка 100 км/ч, то это самое число равно округленно 2*10[sup]5[/sup]
Если с той же скоростью летит Пайпер, то его 1500 миллиметровая хорда гордо рассекает приземный воздух на почти 30*10[sup]5[/sup]
Но это само по себе еще не все. Каждому телу, в частности профилю, еще определяется критическое число. Если я таки чего не напутал, то это то значение, при котором ламинарное обтекание (такое плавное и журчащее 🙂 ) переходит в турбулентное ( бушующее и клокочащее). И тогда, профиль, который стоял на модельке и прекросно её носил, при увеличении в 15 раз может совершенно испортится и наоборот. Но дальше начинаются дебри.
Допустим тот же Пайпер разогнался до 205 км/ч. И числа Рейнольдса его профиля стали 60*10 [sup]5[/sup]. Если, так умозрительно, критическое чило какого нибудь 1500мм профиля было рассчитано на ламинарное обтекание на 51 км/ч, то 205 превышает это значение в 4 раза. Исходя из формулы, переход на турбулентное обтекание начинается на 1/4, т.е. 25% профиля.
Если еще разогнаться, то еще на более меньшем участке носа будет ламинарное обтекание.
Но вот что это мне дает или отнимает никак не пойму. Тем более в трапециевидном крыле, где при одной и той же скорости имеем разные по значению числа. Хорды же меняются по размаху. 😱
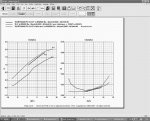
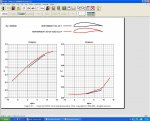
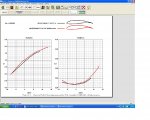
К примеру есть "симпатичный" Вортман FX-63-137. Но у него крайне низкие критические числа. НА моделях должен отлично проходить, а на том же Пайпере? Если допустим крыло пластиковое и в точности повторяет теоретический профиль, но фактически весь находится в зоне турбулентости? И все его достоинства ламинарной геометрии попросту не работают или все же дела обстоят как то иначе?
Порыл в статистике применения этих профилей. Вообще не густо, казалось бы логично. Но с другой стороны есть несколько моделей серийных мотопланеров Катаны и Димоны с этим профилем и хордой порядка 1000 мм. Но даже с такой хордой на реальных скоростях за 100 км/ч, числа Рейнольдса совсем не радужные.
Значит Катаны плохо летают? Или старина Рейнолдс чего напутал 😀?
Объясните, плиз, чайнику на пальцах основы высшей аэродинамики :-/
Если я правильно понимаю суть вопроса, то для любого тела с любыми размерами, двигающегося в любой среде кроме вакуума, существуют эти самые числа. Они меняются в зависимости от собственно этой среды, её вязкости. И еще определяющими является скорость движения и размер тела. Для воздуха, если сильно высоко не забираться есть простая формула Re=70*V*L.
Где L - к примеру хорда крыла, в миллиметрах; V - соответственно скорость в м/с. А само число вообще безразмерное.
Т.е. если модель с хордой 100 мм летит со скоростью порядка 100 км/ч, то это самое число равно округленно 2*10[sup]5[/sup]
Если с той же скоростью летит Пайпер, то его 1500 миллиметровая хорда гордо рассекает приземный воздух на почти 30*10[sup]5[/sup]
Но это само по себе еще не все. Каждому телу, в частности профилю, еще определяется критическое число. Если я таки чего не напутал, то это то значение, при котором ламинарное обтекание (такое плавное и журчащее 🙂 ) переходит в турбулентное ( бушующее и клокочащее). И тогда, профиль, который стоял на модельке и прекросно её носил, при увеличении в 15 раз может совершенно испортится и наоборот. Но дальше начинаются дебри.
Допустим тот же Пайпер разогнался до 205 км/ч. И числа Рейнольдса его профиля стали 60*10 [sup]5[/sup]. Если, так умозрительно, критическое чило какого нибудь 1500мм профиля было рассчитано на ламинарное обтекание на 51 км/ч, то 205 превышает это значение в 4 раза. Исходя из формулы, переход на турбулентное обтекание начинается на 1/4, т.е. 25% профиля.
Если еще разогнаться, то еще на более меньшем участке носа будет ламинарное обтекание.
Но вот что это мне дает или отнимает никак не пойму. Тем более в трапециевидном крыле, где при одной и той же скорости имеем разные по значению числа. Хорды же меняются по размаху. 😱
К примеру есть "симпатичный" Вортман FX-63-137. Но у него крайне низкие критические числа. НА моделях должен отлично проходить, а на том же Пайпере? Если допустим крыло пластиковое и в точности повторяет теоретический профиль, но фактически весь находится в зоне турбулентости? И все его достоинства ламинарной геометрии попросту не работают или все же дела обстоят как то иначе?
Порыл в статистике применения этих профилей. Вообще не густо, казалось бы логично. Но с другой стороны есть несколько моделей серийных мотопланеров Катаны и Димоны с этим профилем и хордой порядка 1000 мм. Но даже с такой хордой на реальных скоростях за 100 км/ч, числа Рейнольдса совсем не радужные.
Значит Катаны плохо летают? Или старина Рейнолдс чего напутал 😀?
Объясните, плиз, чайнику на пальцах основы высшей аэродинамики :-/