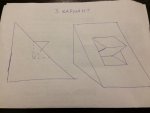
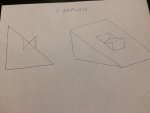
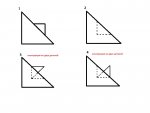
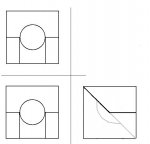
Ошибаетесь, [highlight]найдено только два решения[/highlight] и мои два бесконечные множества решений с цилиндрическими поверхностями.
Очевидно, что до этого Вы не додумались в своих остальных вариантах.
Остальные якобы ответы содержат невидимые линии которые маскируются ребрами.
По правилам черчения в таких случаях
ОБЯЗАТЕЛЬНО делают местные вырывы или дополняют дополнительными сечениями.
Хотя если проанализировать Ваши ещё не озвученные варианты, то может оказаться, что более двух решений Вы не смогли найти.
Вам как проверяющему
не зачет.
Если
всякий проверяющий будет допускать по две ошибки в четырех задачах, то это уже не проверяющий.
Как Вы думаете, сколько балов поставит преподаватель ученику, который не решил правильно две задачи из заданных четырех? Причем, эти задачи однотипные.
Так чего же Вы с такой подготовкой взялись за роль судьи?