Беседы о теории машущего полёта.

[DesertEagle]

Такое ощущение, что многие махолетчики живут в 16 веке, когда еще не было изобретено фотоаппаратов, не говоря уж про базовые понятия из аэродинамики.

Что, так сложно найти видео полета какой-нибудь птицы, сделать оттуда несколько кадров да самому посмотреть, раз уж не верите тому что пишут умные люди в книгах про птиц, начиная с полутора столетий назад (с Отто Лилиенталя)?

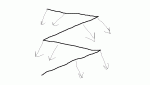
Длины стрелок для двух сечений, примерно в середине крыла и ближе к кончику, я нарисовал от балды, но думаю принцип должен быть понятен. Синяя стрелка вперед у обоих сечений одинаковая, так как это скорость полета птицы. Зеленая на кончике длиннее, так как окружная скорость кончиков выше.

Реальная скорость движения сечения крыла относительно воздуха получается по голубой стрелке. Именно это направление набегающего потока, и именно относительно него строятся углы атаки. А теперь смотрим под каким углом к потоку идет каждое из этих двух сечений и делаем выводы.

А теперь вопрос персонально к KarpovAndrey, ну и чему получились равны углы атаки, отмеченные красным, в конкретно этот момент маха? Ну там близко к 10 град, а может 90 град, а может -20 град? А теперь домашнее задание: взять реальные значения скорости полета конкретной птицы и ее частоту махов. И аккуратно нарисовать такие вектора, соблюдая их реальные длины, для каждого сечения в каждый момент маха.

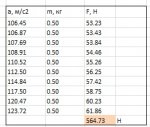
И, о чудеса науки, оказывается, можно не просто их рисовать, а еще и по формулам аэродинамики найти длины стрелок подъемной силы и лобового сопротивления, которые привязаны к этим векторам воздушных скоростей. И определить на их основе создаваемую птицей подъемную силу конкретно в граммах/килограммах. Да, я понимаю, что для большинства махолетчиков это открытие сейчас было как гром среди белого дня, но что делать, с тех пор как вы остановились в развитии, наука ушла далеко вперед. Более того, оказывается можно сравнить полученный результат с известным весом птицы. Проверив таким образом правильность расчета. А то мало ли, вдруг формулы аэродинамики не подходят для живой птицы? Обязательно надо сравнить. После этого можете убрать из формул движение вперед-назад (вашу любимую восьмерку) и сделать расчет чисто для движения крыла вверх-вниз. И сравнить результаты, выявив таким образом вклад восьмерки в общие аэродинамические силы при машущем полете. И удивиться.

Более того, эти же стрелки и скорость их перемещения, нарисованные прямо на птице из любого видеоролика, однозначно определяют мускульную мощность, затрачиваемую птицей на махи и на полет. Пожалуйста, махолетчики со слабым здоровьем, не делайте таких расчетов. Потому что я представляю какой для вас будет удар полученные цифры. Еще бы, столько лет удивляться эффективности птичьего полета, читая рассказы специалистов, которые одинаково специалисты как в машущем полете, так и в пользе шапочек из фольги для защиты от излучения американских спецслужб; травить умильные байки с товарищами про 1.8 Вт затрачиваемой мощности в полете у 12 кг гуся, охать и ахать, мечтая познать тонкости нестационарной аэродинамики, дающей птицам такие потрясающие характеристики. А тут любой видеоролик из интернета, карандаш и знания из второго класса (или когда там школьники начинают проходить про синусы и косинусы?), оказывается, все расставляют по местам. Понимаю, не каждый выдержит такое потрясение. Так что пожалуйста махолетчики, не надо так делать. Не рисуйте никаких векторов на птицах и не делайте никаких расчетов, поберегите себя.

 

[DesertEagle]

Продолжим базовый ликбез. По задачке, решение которой махолетчиками я что-то не увидел.

Итак, если у вас есть картинка птицы из видео ее горизонтального полета с кадрами в крайних точках махов, а также вы знаете массу птицы (1.5 кг), ее размах (1.3 м) и частоту махов (2 Гц), то этих данных достаточно для определения ее мускульной мощности, затрачиваемой на махи при полете.

Распространенной ошибкой махолетчиков, послужившей источником мифов про сверхэкономичность машущего полета, является рассмотрение птицы как материальной точки. Действительно, раз птица создает подъемную силу L, то мы имеем право приложить среднее значение подъемной силы к корпусу птицы.

Вниз тянет сила тяжести F=m*g = 1.5 кг * 9.8 м/с2 = 14.7 Н , вверх тянет подъемная сила L. И они равны друг другу. Так как из видео мы видим, что во время маха положение центра масс почти не меняется, то есть L во время махов примерно постоянна и примерно равна весу птицы L = F.

Однако из видео мы видим, что при махе вниз корпус (центр масс) все же немного поднялся на высоту h.

А как все знают, один киловатт мощности это подъем примерно 100 кг на высоту один метр за 1 секунду.

Из видео мы видим, что центр масс чайки во время каждого маха поднимается примерно на 6 см за 0.25 сек (при частоте махов 2 Гц). Что дает вертикальную скорость подъема корпуса v=h/t=0.06 м / 0.25 сек = 0.24 м/с. Отсюда получается затрачиваемая 1.5 кг чайкой мощность в полете N=F*v= 14.7 Н * 0.24 м/с = 3.5 Вт.

Правильно? Нет, не правильно.

Потому что подъемная сила в полете вовсе не приложена к корпусу чайки. Она распределена, в первом приближении, равномерно по крылу. Примерно вот так:

Вниз по-прежнему тянет сила тяжести F=m*g, а вверх каждое крыло тянет подъемная сила, равная половину веса птицы, L/2. Вместе на обоих крыльях они составляют полную подъемную силу, равную весу птицы L = F.

Что ж, равномерно распределенную силу мы имеем право заменить средней равнодействующей силой, которая расположена примерно на середине крыла (в реальности ближе к кончику, но это зависит также от сужения крыла и распределения при махах). Вот так:

Что же наблюдательный читатель может увидеть на этой картинке? А то, что птица при каждом махе вниз перемещает эту равнодействующую силу L/2 на расстояние h, причем против направления вектора L/2. Подъемная сила L/2 во время всего маха остается примерно постоянной, как мы уже выяснили по поведению центра масс (иначе он бы сильно колебался по высоте, а на видео этого явно не происходит).

Зная размах крыльев чайки 1.3 м, легко находим, что h равна примерно 35 см, т.е. h=0.35 м. Значит вертикальная скорость перемещения  равнодействующей при частоте махов 2 Гц, равна v=h/t=0.35 м / 0.24 м/с = 1.46 м/с.

Вот теперь мы можем узнать мускульную мощность птицы, с которой она машет крылья и которая требуется для машущего полета (умножаем на 2, так как у нас два крыла).

N = F*v = 2*(L/2)*v = 2*(14.7 Н / 2) * 1.46 м/с = 21.46 Вт.

Итак, затрачиваемая мускульная мощность 1.5 кг чайкой для маха вниз, равна 21.46 Вт. Что дает удельную мощность к ее весу, 21.46 Вт / 1.5 кг = 14.3 Вт/кг.

В точности с описанной биологами аэробной метаболической мощностью птичьих мышц (10-20 Вт/кг в длительном режиме, в зависимости от массы птицы).

А как же, спросите вы, колебания корпуса птицы по высоте? Как птица может развивать при махах 21.46 Вт? У нее нет никакой опоры в воздухе, значит она должна была эту мощность передать к крылу согласно определению 1 кВт = подъем 100 кг на 1 м за 1 сек?

Для этого надо посмотреть на устройство птичьего крыла.

В нем имеются жесткие кости лонжерона крыла и жесткая кость грудной клетки, соединенные через шарнир. Птица мышцами тянет одно к другому. Получается своего рода силовой треугольник. Как видите, это не привязано к весу птицы или еще чему либо. Нет никаких препятствий тянуть мышцами кость крыла к кости грудной клетки с таким усилием F и такой скоростью v, чтобы это давало нужную нам мощность N=F*v.

Для самых сообразительных - а теперь сравните с плоско-параллельными махами (раскачивание на трапеции дельтаплана). Каким образом там передается мощность к крылу? Найдите отличия и сравните амплитуду вертикальных раскачиваний пилота в птичьем приводе и в плоско-параллельном.

Ну хорошо, скажете вы. Но птица по-прежнему ни на что не опирается в воздухе, эта передаваемая крыльям мощность все равно должна каким-то косвенным образом отражаться на колебания центра масс согласно согласно 1 кВт = подъем 100 кг на 1 м за 1 сек?

Да с чего бы. Вы же сами видите из видео, что во время маха центр масс почти не сдвигается. Значит подъемная сила во время маха остается примерно постоянно и примерно равной весу птицы. Нет там никаких колебаний, система уравновешена. (а теперь сравните с плоско-параллельным приводом).

Ну ладно-ладно, а куда же тогда тратится вся эта прорва мощности? И почему чайка не может полететь, например со скоростью 800 км/час, а летает на 50 км/час? Из картинок выше это ограничение на скорость полета никак не следует.

А для этого надо посмотреть на птицу сбоку. Подъемная сила это только вертикальная составляющая полной аэродинамической силы R. При махе вниз большая ее часть наклонена вперед, создавая тягу для полета T. В равномерном полете тяга уравновешивает лобовое сопротивление птицы X. Эти две средние суммарные силы в птице равны друг другу, как и в любом ЛА или любом движущемся объекте в любой среде.

Вот куда тратится мощность - на горизонтальное движение. Чем быстрее надо лететь, тем больше воздушное сопротивление Х и тем больше надо наклонять при махе вниз полную аэродинамическую силу R вперед, чтобы создать тягу Т, равную Х. А мускульная мощность чайки ограничена, ее хватает только до скорости 50 км/час.

Для маха вверх, думаю, без труда проведете аналогичные построения, только учтите меньший угол атаки при махе вверх. И как следствие, длины всех стрелок окажутся меньше по величине (и углы наклона будут на угол аэродинамического качества на этом угле атаки).

Дальше посчитать так для каждого участка крыла и всех моментов махов, и найти средние величины за время всего полета, дело десяти строчек в экселе.

Итак, у меня вопрос к махолетчикам. Какого ... вы страдали столько лет х#рней.  У вас не было видеоролика с полетом чайки, вы на youtube забанены что ли? Или вы не понимаете как строятся вектора сил? Не знаете как найти его модуль или проекцию на ось? Не изучали в школе что такое синус что ли? Прям теряюсь в догадках, что могло помешать в течении двадцати лет взять в руки карандаш, нарисовать несколько стрелок и найти затрачиваемую мускульную мощность птицы, конкретно в Вт.

Зачем было вешать на уши лапшу про какие-то вихри, нестационарности, про то что машущий полет в несколько раз экономичнее самолетного. Когда затрачиваемая мускульная мощность птиц определяется непосредственно из любого видеоролика.

 

[lav]

lav писал(а) 27.12.14 :: 19:10:59:
Но откуда у Вас взялся такой вывод ? " в машущем режиме нет никакой нестационарности"?!!!

Нестационарность - это когда величина силы зависит от того что было в предыдущий момент времени. Вот махнула рыба плавником - а к этому маху примешивается вихрь от предыдущего маха, имеем нестационарность (у насекомых так же). Потому что если это первый мах, то получаются одна сила по величине. А если это второй мах в серии, то совсем другая.

Если же систему можно разбить на сколь угодно малые отрезки времени и силы в каждом не зависят от того, что было в предыдущем отрезке времени. Если каждый такой отрезок времени мы можем рассматривать отдельно и независимо. То такая система называется стационарной. Ну или квазистационарной, что одно и то же.

И неважно сколько вихрей при этом генерируется, по какой траектории движется крыло. Это может быть движение с ускорениями, с дополнительной эжекцией по сравнению с неподвижными крыльями, что угодно. Если движение можно разбить на короткие отрезки времени и считать силы в каждом независимо от других участков (находить среднее перемещение за время этого отрезка, мощность по N=F*v и т.д.). То такая система называется стационарной.

Прежде всего необходимо определиться со стационарностью! По определению в стационаром режиме в каждой точке пространства взаимодействия (перед крылом и в кильватерном следе) линии тока неизменны во времени в течении всего  времени наблюдения , этот режим возможен только при условии отсутствия изменения циркуляции (отсутствии изменения ПС). При любом  изменении циркуляции вокруг крыла начинается переходный нестационарный процесс как в кильватерном следе так и в индуцированном потоке перед крылом .При плавных изменениях циркуляции вокруг крыла с задней кромки происходит непрерывный сход элементарных  вихрей вихревой пелены… при резких ,ступенчатых изменениях циркуляции в точках реверса скорости (например при машущем режиме) происходит сход (отрыв) сосредоточенного вихря или системы вихрей обусловленных изменениями происходящими  в пограничном слое! Эти переходные процессы обусловлены необходимостью соблюдения постулата Жуковского-Кутта об одинаковости и непрерывности скоростей струй (над и под крылом) сходящих с задней кромки и первой теоремы Гельмгольца о неизменности циркуляции…как следствий закона сохранения энергии.
Ещё раз в нестационарном  (неустановившемся…  с определённым временем переходного процесса ) процессе все скорости неустановившиеся…не достигшие  максимума…а в отношении индуктивных скоростей это особенно важно ибо они определяют величину кинетических потерь энергии ..определяют величину эффективного АК. Таким образом говорить о стационарности, делать какие либо вычисления в этом режиме(претендуя на точность) можно только при отсутствии каких либо переходных процессов (нестационарнос тей)  …вычисления подобно описанных Вами могут дать приемлемую точность только в случае с достаточно (сравнительно) медленным изменением режима и тогда этот процесс называется квазистационарным!
Способ DPIV применённый в этой работе подтверждает сказанное…чем далее режим от крейсерского тем большее несоответствие  вихревой теории ( теории Жуковского ) наблюдается….[highlight]Су более 2 у воробьиных не может быть объяснён только циркуляционной  ПС…он ,  как минимум, раза в 3 превышает Су воробьиного крыла в стационарном режиме.!
[/highlight]

 

[DesertEagle]

Прежде всего необходимо определиться со стационарностью! По определению в стационаром режиме в каждой точке пространства взаимодействия (перед крылом и в кильватерном следе) линии тока неизменны во времени в течении всего  времени наблюдения

Верно. Стационарный.

описанных Вами могут дать приемлемую точность только в случае с достаточно (сравнительно) медленным изменением режима и тогда этот процесс называется квазистационарным!

Неверно. Квазистационарным называется не медленный процесс (хотя чаще всего медленные процессы являются квазистационарными), а тот у которого маленькие промежутки времени можно рассматривать по отдельности как стационарные, и они не зависят от того что было на предыдущем шаге. А вот если результат на текущем отрезке зависит от предыдущего шага, то это нестационарный процесс. Проще говоря: если в таких же условиях с другим предыдущим шагом изменяется результат, то это нестационарный. При этом машущий полет может иметь плюсы в виде уменьшения индуктивного сопротивления за счет увеличения ометаемой поверхности (ваш любимый прямоугольник биплана) и любых других подобных эффектов. Оставаясь квазистационарным.

Допустим, если в середине маха есть маленький участок длительностью 0.1 сек, в котором воздушная скорость равна 10 м/с, а угол атаки 5 град. Если создаваемые на этом участке аэродинамические силы при махе вниз и махе вверх разные, то машущий процесс нестационарный. Если одинаковые, то квазистационарный.

Про воробьев ничего не могу сказать, в отрывке не указано для какой скорости полета. В тех статьях, которые я читал, утверждалось о полном отсутствии нестационарных эффектов у воробьев и соловьев, начиная со скорости 4 м/с. На более медленной и при зависании есть, но слабо изученные. И в любом случае, требуют больше мощности, чем на скоростях выше 4 м/с, где их нету.

 

[DesertEagle]

Вашу же схему, предложенную к обсуждению, проще пока отложить. 

Схема вполне себе хорошая, имеет много достоинств. Но чтобы так полететь, надо сразу закладывать моторный привод (~5 л.с. для начальных подскоков). А на руки оставить только управляющие воздействия. По изменению угла атаки при махах и для управления. Ноги, в силу их слабости (что тех 200-300 Вт на фоне необходимых для полета 5 л.с.?), можно не подключать, толку от них ноль.

 

[slavka33bis]

1). ...Летает.. и   ...Не летает...,  абсолютно разные вещи.

2). Именно ваша модель может ...не летать .. из за сотни причин.
.

1). Вещи-то разные, но основных причин
              (при том, что частота махов вполне достаточна)
     может быть тоже две.

          а)  недостаточно мощности двигателя;
          б). не правильная конструкция крыльев.

     И может быть совокупность этих двух причин.

2).  Вот именно.
       А просмотр видео даст ответы сразу на большую часть вопросов.

Вы наверное телепат, раз Монтану сразу поняли.
Или в личке перебросились парой сообщений.

А по поводу "сколько моделек изготовил?" не важно это вообще.

Кто, чего и сколько сделал.

Вон Топоров понаделал кучу поделок и что толку ???

Велков тоже что-то стряпает, но это ему не помогает понять как именно должен выглядеть орнитоптер 
и какую именно конструкцию должны иметь крылья и как они должны работать, что бы этот орнитоптер смог полететь.

История уже давно коллекционирует такие же поделки авторов, которые не понимали и до сих пор не понимают сути создания крыльями орнитоптера и подъёмной силы и тяги.
И того, сколько мощности к этим крыльям требуется подвести.

 

[DesertEagle]

Всего существует шесть основных моделей расчета махолета: статическая, динамическая и четыре аэродинамических. Каждая ступень увеличивает сложность и повышает точность расчета.

1. Статическая модель. Это то, что мы чуть раньше рисовали - вектора на крыльях с силами. Движение рассматривается только равномерное, основная формула N=F*v. Просто, наглядно и обладает достаточной точностью.

2. Динамическая модель. Здесь учитываются ускорения и перемещение центра масс по вертикали при махах. А также учитывается инерция. Дает большую точность в определении потребной для полета мощности (в основном, за счет учитывания инерции). Основная формула F=m*a.

3. Аэродинамическая импульсная теория. Здесь оперируют размахом крыльев и ометаемым объемом (то что приводил раньше Анатолий). Недостаток в том, что реальная ометаемая поверхность неизвестна, ее можно оценить лишь примерно. Но зато этот метод позволяет оценить кпд машущих крыльев как движителя. Основная формула F=(m/t)*v (v- не скорость полета, а скорость отбрасывания струи, формула реактивной тяги).

4. Аэродинамическая через эмпирические коэффициенты Cy, Cx. Крыло разбивается на маленькие участки, для каждого по аэродинамическим формулам находится подъемная сила и сопротивление. Эта модель очень проста в реализации, чем-то похожа на статическую, но за счет разбиения времени на короткие отрезки, позволяет также учесть ускорения. Недостаток в том, что нужно знать поляры от близких по геометрии крыльев. То есть знать внешние эмпирические коэффициенты Cy, Cx. И имеются сложности с определением индуктивного сопротивления (оно не очень точное). Но в целом, эта модель позволяет провести полный аэродинамический расчет любого махолета и определить распределение подъемной силы по крылу. Основная формула Lift(Drag) = Cy(Cx)*p*S*v^2/2.

5. Циркуляция по Жуковскому с помощью панельного метода дискретных вихрей. Эта модель не требует знать каких-то внешних данных, она полностью рассчитывает махолет исходя только из его геометрии. Учитывает V-образность крыльев, конечность удлинения, вид профиля (только по его средней линии, правда), а также взаимовлияние крыльев, если используется тандемная компоновка. Это наивысший из аналитических методов расчета. Его используют в научных работах, при проектировании машущих микро-бпла, при сравнении полученных в аэродинамических трубах характеристик живых птиц с расчетными значениями и т.д.

6. Численное решение уравнений навье-стокса с помощью метода конечных элементов. Это все тяжеловесные пакеты CFD, расчеты на суперкомпьютерах и т.д. Идея в подсчете переноса массы и импульса жидкости между элементарными объемами пространства (или прямым переносом массы частицами в вариации уравнений Больцмана). Это наивысшее достижение в аэродинамике и гидродинамике. Учитывает нестационарные эффекты, поэтому подходит для расчета насекомых и мелких птиц типа колибри на режиме зависания. Используется в научных работах по насекомым, и иногда сравнивается с результатами, полученными по пункту 5. Недостаток в медленности расчета, большой зависимости от качества подготовки исходных данных и сложности пакетных расчетов для оптимизации конструкции.

На какой ступени остановиться - решать вам. На практике, самый первый способ обеспечивает вполне достаточную точность для проверки на птицах и для расчета полноразмерного махолета. Второй, третий и четвертый служат, в основном, для более глубокого понимания машущего полета. Если же вы занимаетесь научной работой или пишете диплом, например. То у вас выбор только между пятым и шестым методом, причем с приоритетом в сторону шестого, но с необходимостью реализовать и пятый для проверки и сравнения результатов. Он часто служит валидационной моделью для шестого.

 

[KV1237542]

Ометаемая площадь для голубя в том опыте: если брать траекторию некого фокуса крыла на 0,66 размаха может выглядеть примерно так:

1 ометаемые площади для каждого маха не накладываются

2 К началу следующего взмаха максимальная индуцированная скорость струи от предыдущего вероятно значительно затухает они разнесены и во времени

3 Вдобавок это все происходит при разных размахах крыла при взмахе вверх оно полусложено

4 не знаю насколько удачно нарисовал: воздух будет отбрасываться не прямо перпендикулярно траектории, а несколько под углом учитывая большие углы атаки крыла, что еще уменьшает нахлест площадей, а составляющая скорости которая горизонтальная используется в махе в противоположную сторону

5 Вдобавок это все происходит при разных размахах крыла при взмахе вверх оно полусложено


сравните со сплошным диском ометаемой площади вертолета

Такую прореженность траектории  в отличие от вертолета голубь может позволить себе вследствие больших аэродинамических коэффициентов, возникающих вследствие инерции присоединенных масс воздуха

 

[KV1237542]

А вот и наш гусь, любезно предоставленный Николаем, с датчиками давления:

Обратите внимания, что подъемная сила, создается только при махе вниз

Внизу время маха (частота 5 Гц) взлет:

Размах 1,7 м , площадь крыла 0,36м2, вес гуся 4,7 кг.

Берем точку фокуса где-то 0,5...0,6 размаха и считаем средний Су:

Вертикальная скорость точки фокуса 3,5м/с
горизонтальная 8,5м/с

вект сумма - 9,2м/с

с учетом соотношения 0,13с взмах вниз 0,07 вверх подъемная сила должна быть с запасом при махе вниз

Су где-то получается 3,87...

 

[KV1237542]

Далее, обратим внимание на резкий рост давления на конце крыла при начале маха вниз, последний датчик: если главная подъемная сила - циркуляционная то максимум должен плавно нарастать с ростом вертикальной скорости конца крыла и достигать максимума в середине маха вниз а здесь 2 пика 1 -ускорение крыла 2 -ускорение мануса (для этого на взлете и помогает локтевой сгиб)
оба пика - следствие инерционной составляющей ПС

Ничего экзотического:

крыло движется сквозь воздух увлекая его частицы
если крыло движется с ускорением то и частицы с ускорением
а значит сила инерционной ПС = присоединенная масс * ускорение

поскольку в данном случае вектор ускорения перпендикулярен скорости полета поступательная скорость не помеха реализации инерционной ПС, а чтобы она не тянула вниз при махе вверх:
1 супинируем манус, 2 проницаемость перьев (обращаем внимания на датчики при махе вверх: давление околонулевое для этого и нужна проницаемость крыла)

А вот и грубый расчет порядка инерционных сил (присоединенная масса принята как объем слегка сужающегося цилиндра образующая которого трапециевидное крыло гуся)

ВСЁ, ДА СОЖРЕТ МЕНЯ АНАТОЛИЙ!
АРГЕНТАВИС: ЦИКЛИЧЕСКАЯ ЧАСТОТА СУЩЕСТВУЕТ! ПОВЕРЬТЕ

 

[KV1237542]

ОБРАЩАЮ ВНИМАЕНИЕ: НЕ ПРЕТЕНДУЮ НА ТОЧНОСТЬ И СОВЕРШЕННОСТЬ РАСЧЕТА ХОТЕЛОСЬ ПОКАЗАТЬ ПОРЯДОК ЦИФР.

Наверное длительность действия инерционной ПС больше принятой: 0,5 времени взмаха вниз и дает гусю в среднем около 3кг ПС на взлете

Инерционная ПС считалась так: 1 макс угловое ускорение для гармонических колебаний при такой частоте - далее вес прис. массы - момент инерции - сила инерции пиковая - далее средняя

На самом деле угловое ускорение вероятно постоянное но зато 2 пика  -второй от ускорения мануса мануса судя по датчику примерно такой же.

Крыло естественно деформируется упруго и поэтому инерционная ПС действует быстрее циркуляционной но все же не мгновенно

 

[DesertEagle]

И немного про инерциальную силу.

Попробовал грубо прикинуть, размах 4.5 м, хорда 0.9 м, масса ~30 кг, скорость полета ~48 м/с (макс. достигнутая в горизонте), частота махов 2 Гц, амплитуда 55 град, качество на махе вниз 7.5, на махе вверх 5 единиц. Корпус аналог миделя 45х45 см с Cx=0.4, учитывая все торчащие в потоке трубки и элементы конструкции. Массу крыльев я указал 10 кг, с учетом всех усилений наверно так и вышло в итоге? По 5 кг на консоль.

По всему выходит, что аэродинамическая мощность для полета при таких условиях должна быть около 2-2.3 л.с. (мощность надо смотреть на махе вниз, раз мотор машет крыльями напрямую через редуктор. средняя была бы с рекуперацией при махе вверх). И кпд машущих крыльев как движителя достижим на уровне 80-85%.

Однако сила инерции на крыльях в крайних точках более чем в два раза выше, чем подъемная сила! 56 кг на одном крыле при махе вниз, против средней подъемной 24 кг (вектора в точке примерно на 50-60% размаха, то есть в точке равнодействующей, чтобы было удобно сравнивать). А так как преодолевать ее приходится два раза за мах, разгоняя крыло и тормозя потом, то похоже что итоговая потребляемая мощность как раз находится на уровне 7-8 л.с.

Расчет весьма грубый, с рядом допущений и упрощений.

 

[KV1237542]

Где же тогда эта 40% большая подъемная сила у машущих крыльев? Если бы это было так, то птицы реже махали бы крыльями, чем требуется по традиционной аэродинамике. А они машут в точности с ней. Epic fail, как говорится.

Николай, посчитайте Су гуся или Вы его не замечаете?

 

[DesertEagle]

Николай, посчитайте Су гуся или Вы его не замечаете?

На взлете, с углами атаки под 60-80 град? С такими углами самолетная аэродинамика не работает, это нестационарная аэродинамика. Дайте точную анимацию гуся, я могу прогнать ее через CFD методом конечных элементов.

Инерционную составляющую в ваших прикидках я видел, интересная точка зрения. Надо над ней подумать. Но похоже что все аналитические решения в таком режиме полета не очень точны. Иначе бы их применяли для срывной аэродинамики, а как вы сами знаете, для нее нет нормальных решений приемлимой точности.

 

[DesertEagle]

Кстати, помнится был разговор что все птицы в полете машут с одинаковой частотой (разброс не более 1-2%). А вот тут http://jeb.biologists.org/content/175/1/317.full.pdf пишут, что канадский гусь увеличивает частоту махов на 15% при увеличении скорости полета с 50 км/час до 80 км/час. С 3.92 Гц до 4.5 Гц.

Wing beat frequency also increased by 15% (P<0.05) from 235±13 to
270±18 beats/min as velocity increased from 50 to 80 km/h

 

[KV1237542]

На взлете, с углами атаки под 60-80 град? С такими углами самолетная аэродинамика не работает, это нестационарная аэродинамика. Дайте точную анимацию гуся, я могу прогнать ее через CFD методом конечных элементов.

Инерционную составляющую в ваших прикидках я видел, интересная точка зрения. Надо над ней подумать. Но похоже что все аналитические решения в таком режиме полета не очень точны. Иначе бы их применяли для срывной аэродинамики, а как вы сами знаете, для нее нет нормальных решений приемлимой точности.

Да не важно какие углы да аэродинамика нестационарная

Есть лучшее объяснение как Су получается 3,8?

Нельзя плевать на инерционную составляющую Вы же делали опыт с парашютиком.
А у Болдырева на ней вообще весь вывод формул и неплохо сходиться с результатом.

 

[DesertEagle]

Да не важно какие углы да аэродинамика нестационарная

Еще как важно, нет аэродинамических формул для нахождения Сy при углах атаки при махах 80 град. Там процесс нестационарный.

Есть лучшее объяснение как Су получается 3,8?

Относительно чего этот Cy? Относительно каких векторов?

Я же приводил пример вертолета, летящего на скорости 4 м/с. Пусть масса 2000 кг, диаметр 6 м, ометаемая винтом площадь 28 м2. Какой у него получается самолетный Cy? Cy = Y*2/(p*S*V^2) = 2000*2/(0.125*28*4^2) = 71.

Сy = 71!!! Куда вашим птичьим 3.8  ;D

Птица при коротком взлете или медленном полете, когда у нее вектор тяги направлен под углом вверх, подобна вертолету. Поэтому Cy, приведенный к скорости полета, является бессмысленным. А голубь вообще работает как винт, его амплитуда махов почти 180 град, то есть ометает как окружность. Поэтому у него правомерно считать нагрузку не на площадь крыльев, а на ометаемую как у вертолета. Получится 1.5 кг/м2. Что и объясняет его меньшую в 6 энергетику по сравнению с Ми-2, у которого нагрузка на ометаемую площадь 22 кг/м2.

Если же вы попытаетесь найти Cy относительно набегающего потока при движении крыльев, как у крыла самолета, то облом - как я уже сказал, углы атаки там под 60-80 град, поэтому самолетными формулами это не считается. Так как процесс нестационарный и результат не будет соответствовать чистому самолетному срыву при таких углах. Которые более менее предсказывается, но очень неточно.

Есть же работа по изучению Cy/Cx крыльев голубя: http://jeb.biologists.org/content/214/11/1867.full.pdf . Где просто взяли, и экспериментально измерили Cy и Cx на этих углах атаки 60-80 град. Относительно набегающего потока относительно крыльев. Вот что получилось. А и B для маха вверх, C и D на махе вниз. Как видите, максимальный Cy примерно 1.5 как при махе вниз, так и вверх на угле атаки 60 град. На 80 град снижается до 1.0.

При этом обратите внимание, что Cx (Cd на графике) при этом на 60 град тоже около 1-1.5, то есть аэродинамическое качество равно 1. Какое это имеет значение для энергопотребления, не мне вам объяснять.

А ниже измеренная поляра голубя, красная пунктиром для маха вниз, синяя для маха вверх. Как видим, максимальное аэродинамическое качество на угле атаки 25 град.  6.5 единиц при махе вниз и 2.5 при махе вверх.

Ну и что тут экстраординарного? Да, угол максимального качества 25 град это круто. Видимо дело в малом Re и, возможно, нестационарной природе махов при висении. Но ничего фантастического я при этом не вижу. А вы?  😉

И теперь стоит уточнить, что же там за Cy=3.8 у вас получилось, которое я якобы должен объяснить...  😉

 

[KV1237542]

Относительно чего этот Cy? Относительно каких векторов?

  Это уже с учетом векторной суммы скоростей на махе вниз для точки 0,5...0,6 размаха
с учетом того что на махе вверх подъемная сила не создается, как видно из показаний датчиков
Пример с вертолетом хоть куда ;D, только считайте что учтена скорость непосредственно лопастей

 

[slavka33bis]

Очень интересное видео.
Размещаю тут для моих собственных нужд.

http://www.youtube.com/watch?v=8vARD17nQjg&NR=1

 

[DesertEagle]

Очень интересное видео.
Размещаю тут для моих собственных нужд.

http://www.youtube.com/watch?v=8vARD17nQjg&NR=1

Там по ссылке в видео, тоже несколько интересных документов: http://cas.umt.edu/dbs/flightlab/research.php.

Например здесь http://cas.umt.edu/dbs/flightlab/documents/JEB_Jackson_Dial.pdf делались замеры пиковой мощности маховых мышц у нескольких птиц. Я так понял, что это именно максимальная пиковая, при испуге и в рывке при вертикальном взлете.

Нехило так, у мелких птиц до 350 Вт/кг (к массе мышц, а не всей птицы). Даже у вОрона 267 Вт/кг. Хотя у вороны 185 Вт/кг, странно, я думал вОроны крупнее и поэтому у них мощность мышц должна быть меньше. Может средняя и меньше, а пиковая в рывке в вОрона почему-то больше.

Если привести к размеру человека, имеющего примерно 23 кг мышц, то это пиковая мощность 23*350=8050 Вт, или 11 л.с.. Кто-то еще удивляется, почему птицы так легко летают?