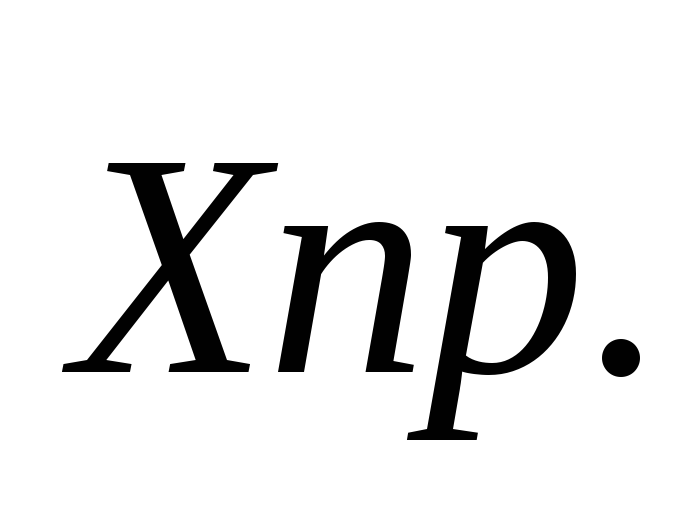Я как-то плохо представляю себе визуализацию решения задачи о продолжении движения двумерного крыла. После задней кромки есть поверхность раздела. Эта поверхность должна искривляться и закручиваться, т.к. есть разница давлений. Не представляю, как это можно "упаковать" в стационарную картину. Можно представить, что по мере ухода центра разгонного вихря в бесконечность его радиус растёт до бесконечности - вот тогда течение в районе задней кромки меняться не будет. Но это значит, в течение всего полёта расходуется энергия на подпитку вихря.
Делается в идеальной жидкости (не будем париться со сжимаемостью для простоты) так:
во-первых, если есть вихрь с циркуляцией Г, то скорость вокруг центра этого вихря на достаточном расстоянии r от центра (вне ядра) будет Г/(2*pi*r)
во-вторых, когда крыло с острой задней кромкой начинает движение, то линия тока сходит не с кромки, а выше неё. На кромке получается бесконечная скорость, эту бесконечность поток, естественно, устраняет (тут как раз требуется вязкость, а мы её исключили из модели). В рамках невязкой модели на задней кромке, чтобы запустить процесс устранения бесконечной скорости, возникает вихрь с бесконечной скоростью вокруг ядра, этот вихрь вскорости срывается с кромки и летит назад. И продолжает увеличивать свою интенсивность, а крыло продолжает набирать подъемную силу. За вихрем потянется поверхность разрыва (в первом томе Прандтля-Титьенса процесс в главе про вихри описан). На поверхности разрыва давление непрерывно, скорость испытывает скачок. Вихрь будет набирать свою интенсивность ровно до тех пор, пока скорости с двух сторон поверхности разрыва не сравняются. Как только сравняются - всё, стационарная подъемная сила для этого профиля, скорости полета и угла атаки достигнута. Потому, что у крыла образуется присоединённый вихрь противоположного вращения и той же интенсивности, что и отходящий. По теореме Томсона суммарная циркуляция должна быть ноль, какой она была пока крыло стояло. На создание этих вихрей и увеличение их циркуляций придется истратить работу даже в идеальной жидкости.
Вообще же, классические представления таковы, что для возникновения этого начального вихря и формирования условия Чаплыгина на задней кромке необходима вязкая жидкость. Правда после его образования вязкость становится уже не нужна. Поэтому так и интересны для теории эти дискуссии про АДТ со сверхтекучим гелием - будет ли возникать условие Чаплыгина вообще без вязкости?
Вот отличный пример расчета начального вихря
Но это ещё не все, потому, что, в-третьих, начальный вихрь начнет наводить скос на крыле. Точно так же, как и в обычной теории крыла конечного размаха и индуктивного сопротивления. У вихря ведь есть поле скорости w = Г/(2*pi*r). Вот эта w и будет наклонять силу, давая сопротивление Х. Это сопротивление легко найти по схеме на картинке
Х=Y*(w/V)=(1/V)*ro*V*Г*(Г/(2*pi*r)=(ro*Г^2/(2pi))*(1/r)=const/r
теперь считаем работу этой силы сопротивления за время, пока стартовый вихрь летит от расстояния до крыла L1 до расстояния L2 как определенный интеграл от L1 до L2 (символ интеграла жирная S)
A = SXdr = const*Sdr/r = const*ln(L2/L1)
Получился логарифм. Если L2 устремить в бесконечность - потребная работа будет бесконечно возрастать с удалением вихря от крыла. Спасает только то, что эта бесконечность логарифмическая, поэтому при больших L2 и L1, когда вихрь улетит достаточно далеко, работа в идеальной жидкости становится бесконечно малой, т.к. L2/L1 становится примерно 1.
Поэтому, когда все "переходные процессы" завершились и крыло летит горизонтально с постоянной скоростью, то мотор тратит мощность только на преодоление сопротивления, созданного путём различных механизмов силами вязкости. В идеальной жидкости он вообще не тратит мощности - создал один раз толчком подъемную силу и вуаля...
извиняюсь за длинноту
UPD/ Думаю, что из формул выше понятно, что, как только начальный вихрь удалится от крыла достаточно далеко, в этой идеальной жидкости сопротивление, как и положено, становится нулевым. А то мало ли что, тут, иногда и не знаешь какой очередной выверт преподнесут...
Последнее редактирование: