Спасибо за борьбу "против" науки...
🙂
А как же Ваша борьба ЗА науку?
Где позитивные ответы на вопрос:
Что сделать, чтоб он сложил только векторы угловых скоростей водила и эксцентрика на нем?
Был бы благодарен...
Или Вы здесь на нашей "ветке РЛД" не благородной благодарности ради, а волею "пославшей-Тя" на [.][.][.] жены? :-?
~~~~~~~~~~~~~~~~~~~~~
---------------------------------
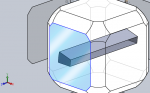
Здесь имеется в виду водило из 2-х, 3-х или 4-х (как на рисунке) параллельно нагруженных "орбитально-планетарных" ветвей...
Орбитально-планетарная кинематика изображена только один раз, - для простоты изображения, другие ветви подразумеваются такими же, из соображений уравновешенности.
Желтым изображена коренная шейка эксцентрика [коленвала], красным - мотылевая шейка. Ось мотылевой шейки смещена от оси коренной шейки на величину эксцентриситета [расстояние между осями маленьких кружков: желтого и красного]
е.
Фактически меня интересует "голубой угол" поворота [положения, скорости и ускорения] этой самой оси относительно (желтого) угла [ch966] синего водила
- с учетом поворота "желтого угла" поворота водила [угла [ch966]]...
- и промежутка времени, в течение которого такие смещения происходят [угловой скорости равномерного "синего вала с синим водилом"].
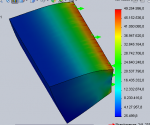
А в конечном итоге нужны графики,
-
как меняется длина и угол РЕЗУЛьтирующего (голубого) вектора, представляющего сумму векторов: желтого радиуса водила + красного вектора угла поворота оси эксцентрика... в зависимости от аргумента [ch966] 😀
- как меняется вместе с ними угловые скорости и угловые ускорения каждого блока лопастей, ведомого своей отдельной мотылевой шейкой эксцентрика.
- при допущении-условии, что есть зависимость между углом поворота водила ([ch966]) и углом поворота вектора из оси коренной шейки в направлении оси эксцентрика.
Эту зависимость можно экспериментально принять одной из ряда возможных:
- эксцентрик вращается быстрее водила в 2 раза,
- эксцентрик вращается быстрее водила в 4 раза,
- эксцентрик вращается быстрее водила в 6 раз ...
Колебания углового положения "голубого вектора" относительно радиуса, направленного на коренную шейку, - от крайнего левого до крайнего правого положения, - задают "угловой ход" одного блока лопастей.
А так как РЛД - в принципе "встречник", то суммарный рабочий ход двух смежных лопастей, определяющий и расчетный рабочий объем РЛД (без учета возможных других факторов), - будет удвоенным ходом "голубых векторов": для левого блока лопастей и правого блока лопастей.
Для одного расчетного примера можно принять отношение R (желтого вектора) водила к величине
e (k красному вектору r) как примерно, почти произвольно назначаемая константа C4: R/e = 4 [или 2, или 6, или др.]
Ну и соотношение угловых поворотов для изображенного, в частности примера, 1: C4. То есть, при вращении желтого вектора против часовой стрелки на 2° от исходного, красный вектор повернется ПО часовой стрелке на 8° [встречно] от исходного [ch966], равного нулю...
Как говорилось, константа C4 может быть просчитана и как C2=2 и как C6=6
🙂 В таком случае разные обозначения константы -> синонимы.
🙂