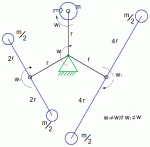
вот miharus привел школярское решение для конкретного положения ротора, что в принципе не доказывает что ротор будет полностью уравновешен при других положениях
Школярское намеренно, т.к. например после слов "момент инерции" коллеги впадают в ступор и сложно отличить от "момент силы", "момент импульса", "момент силы-действия", "момент". Поэтому человеку нужно обьяснять на том языке и понятиях которые он понимает, что возможно, что я и сделал. Другое дело что придется расшифровывать эти школярские уравнения на что они никак не могут решиться.
для конкретного положения ротора, что в принципе не доказывает что ротор будет полностью уравновешен при других положениях
Конкретное положение: " 3) Fаx=Fax1+Fax2+Fax3=
= -Wa^2*Ra*M1*cos(Wa*t+270)-Wa^2*Ra*M2*cos(Wa*t+30)-Wa^2*Ra*M3*cos(Wa*t+150)=
0 (т.к. ротор уравновешен вокруг своей оси a)." - для конкретной картинки в момент t=0.
Была бы картинка с роторм развёрнутым на 180 град в момент t=0, уравнение было бы:
Fаx= -Wa^2*Ra*M1*cos(Wa*t+270)-Wa^2*Ra*M2*cos(Wa*t+30)-Wa^2*Ra*M3*cos(Wa*t+150)=
0 , (этот первоначальный момент мог бы быть и другим) главное что это уравнение всё равно выкидывается, т.к. это дисбаланс ротора на своей шейке, а он равен =
0.
Что касается "что в принципе не доказывает что ротор будет полностью уравновешен при других положениях..."...
какие ещё могут быть положения, если в уравнениях переменные: Wa, Wb, Ra, Rb=e, M, t ; подставляйте любые скорости, массы, радиусы, углы (Wa*t=альфа(град), Wb*t=бетта(град), любые сочетания Wa/Wb, пусть ищут резонансные положения или что они вообще ищут. Уравнения для всех характеристик в любой момент времени. Калькулятор в руки.
(Извиняюсь что не написал уравнения проеции сил на Х для балансира(на осн. валу), исправляюсь (для рисунка):
Fx(t)бал=-Wb^2*Rb*M1*cos(Wb*t+90)-Wb^2*Rb*M2*cos(Wb*t+90)-Wb^2*Rb*M3*
cos(Wb*t+90)=
= Fx(t)=-Wb^2*Rb*(3*M)*cos(Wb*360/(2*"Пи")*t+90), либо => Мбал*Rбал=3*М*Rb ,
думал что это очевидно. И под "cos(углы в градусах)" как в последнем уравнении.)