Роторные двигатели - идеи и критика.

[EX-62]

Кажды детайль которы крутится, делаются баланс на стенде. Если у теоритиков не получается баланс = 0, они поставит в формуле коефиценты (у нас  называется  коефициенты незнание ;D).

 

[Андрей Миллер]

у насназываетсякоефициенты незнание 

У них и со знаниями - 0... ;D

 

[martensito]

По отношению к оси статора, или Вы плохо видите схемы (пост 1925), выложенные ЕХ-62?
Любое планетарное движение рождает уравновешенный или неуравновешенный дисбаланс. И это хорошо видно на схемах.

непонятные ветряные мельницы с пропеллерами на концах пропеллеров...

а умеют ли они их вообще читать, или та только смотреть в них и видеть ....... ;D

 

[miharus]

По отношению к оси статора, или Вы плохо видите схемы (пост 1925), выложенные ЕХ-62?
Любое планетарное движение рождает уравновешенный или неуравновешенный дисбаланс. И это хорошо видно на схемах.

непонятные ветряные мельницы с пропеллерами на концах пропеллеров...

а умеют ли они их вообще читать, или та только смотреть в них и видеть ....... ;D

Где хоть одно български слово про дисбаланс (пост 1925), его оценки, графические оценки его величины? Братушка, буди добр, цитатку из текста вытащи про балансировку?
Я так понял из рисунков, они посвящены тому что нужно правильно расчитывать "первоначальное" взаимное расположение системы:  ротор-вал-статор, чтобы в фазу сжатия-вспышки происходило "смещение" в подшипниках (на велелечину зазора, что неизбежно) ротор-вал и вал-статор (правильное расположение на предпоследней картинке), но при этом не происходило (минимизировать) одновременное "смещение+поворот (об шестерню)" от сжатых газов, которое возможно и показаны такие эффекты на первых двух рисунках.

АААтличные рисунки. Господа рисователи, поднатужтесь и точечками, эксцентриситетами, стрелочками, хоть как-то НАРИСУЙТЕ дисбаланс хотябы на какой-то фазе (или можно взять за основу любой из десятка предыдущих прекрасных рисунков, ведь ими Вы "что-то убедительно доказали"). Расчётов, уравнений у меня нет наглости просить, ведь профессионалу "достаточно вообще читать" рисунок, рисовать рисунок, обсуждать рисунок, коментировать рисунок, ну Вот-же! Вот! из рисунка-же всё понятно! Ну и главный аргумент правоты:  ;D

 

[МаГент]

Любое планетарное движение рождает уравновешенный или неуравновешенный дисбаланс. И это хорошо...

Миллер, любое ваше высказывание рождает уморительную "дисбалансную физику"! Умоляю, не останавливайтесь, это ж просто "нашараша" какой-то... ;D

Инструкцию к Вашей голове?

А что, вы своей по инструкции пользуетесь? Где скачивали? Ссылочку можно, похоже перевод неправильный, видимо с китайского, у вас там какие-то кнопочки перепутаны.... :🙂

 

[Андрей Миллер]

профессионалу "достаточно вообще читать" рисунок, рисовать рисунок, обсуждать рисунок, коментировать рисунок, ну Вот-же! Вот! из рисунка-же всё понятно! Ну и главный аргумент правоты: 

Профессионалу достаточно понимать все схему в уме. 🙂
Рисунок нарисую как только появится время. Нельзя же дать помереть РПДистам в невежестве... 🙁

 

[martensito]

Чтобы не заморачиваться с рисованием векторов сил,  уравнения для проекций сил на оси Х и У.

Точки a=Ш, b=К, массы М1=М2=М3=М, их сумма = 3*М, массы "ротора жесткого трехточечного" вращаются вокруг оси а с частотой Wa (и r=Ra); сама ось а вращается вокруг оси b с частотой Wb (и r=Rb).

1) Найдем проекцию на ось Х равнодействующей F(t) сил (от движения масс с ускорением) приложенные к точке b :
Fx(t)=Fx1(t)+Fx2(t)+Fx3(t); (далее (t) опускаем для краткости, а рисунок берем за положение системы при t=0)

2) раскладываем ускорения движущихся масс (М1, М2, М3) и соотв. силы на составляющие (уравнения их проекций на Х):
2а) Fx1=Fax1+Fbx=-Wa^2*Ra*M1*cos(Wa*t+270)+(-)Wb^2*Rb*M1*cos(Wb*t+270);
2б) Fx2=Fax2+Fbx=-Wa^2*Ra*M2*cos(Wa*t+30)+(-)Wb^2*Rb*M2*cos(Wb*t+270);
2в) Fx3=Fax3+Fbx=-Wa^2*Ra*M3*cos(Wa*t+150)+(-)Wb^2*Rb*M3*cos(Wb*t+270).

3) Fаx=Fax1+Fax2+Fax3=
= -Wa^2*Ra*M1*cos(Wa*t+270)-Wa^2*Ra*M2*cos(Wa*t+30)-Wa^2*Ra*M3*cos(Wa*t+150)=0 (т.к. ротор уравновешен вокруг своей оси a).

4) складываем уравнения 2а), 2б), 2в) и с учётом уравнения 3) имеем:
Fx(t)=Fx1+Fx2+Fx3=-Wb^2*Rb*M1*cos(Wb*t+270)-Wb^2*Rb*M2*cos(Wb*t+270)-Wb^2*Rb*M3*cos(Wb*t+270)=
=    Fx(t)=-Wb^2*Rb*(3*M)*cos(Wb*t+270)

С проекциями на ось У аналогично (с заменой "cos" на  "sin") и т.о:
 
"Трехточечный ротор" нужно рассматривать как одну точку с массой 3М=М1+М2+М3
вращающуюся вокруг оси b на расстоянии Rb с частотой Wb, и соответственно уравновешивать эту массу противовесом.
Т.е. сажаем на основной эксцентриковый вал "ротор", балансиры для уравновешивания "3М", а оборотов ротора Wa в конечной формуле нет. Как же так? 🙁 
Какая печалька для алхимиков дисбалансов из-за особых "разнооборотных сочетаний  магических положений ротор-вал"  ;D

может расчеты надо подкорректировать  😉

 

[miharus]

может расчеты надо подкорректировать  😉

Ваш сканер перепутал страницу, или книгу, или тему, или форум, или читать не умеет, ЕГО надо подкорректировать. :STUPID

 

[martensito]

Чтобы не заморачиваться с рисованием векторов сил,  уравнения для проекций сил на оси Х и У.

Точки a=Ш, b=К, массы М1=М2=М3=М, их сумма = 3*М, массы "ротора жесткого трехточечного" вращаются вокруг оси а с частотой Wa (и r=Ra); сама ось а вращается вокруг оси b с частотой Wb (и r=Rb).

1) Найдем проекцию на ось Х равнодействующей F(t) сил (от движения масс с ускорением) приложенные к точке b :
Fx(t)=Fx1(t)+Fx2(t)+Fx3(t); (далее (t) опускаем для краткости, а рисунок берем за положение системы при t=0)

2) раскладываем ускорения движущихся масс (М1, М2, М3) и соотв. силы на составляющие (уравнения их проекций на Х):
2а) Fx1=Fax1+Fbx=-Wa^2*Ra*M1*cos(Wa*t+270)+(-)Wb^2*Rb*M1*cos(Wb*t+270);
2б) Fx2=Fax2+Fbx=-Wa^2*Ra*M2*cos(Wa*t+30)+(-)Wb^2*Rb*M2*cos(Wb*t+270);
2в) Fx3=Fax3+Fbx=-Wa^2*Ra*M3*cos(Wa*t+150)+(-)Wb^2*Rb*M3*cos(Wb*t+270).

3) Fаx=Fax1+Fax2+Fax3=
= -Wa^2*Ra*M1*cos(Wa*t+270)-Wa^2*Ra*M2*cos(Wa*t+30)-Wa^2*Ra*M3*cos(Wa*t+150)=0 (т.к. ротор уравновешен вокруг своей оси a).

4) складываем уравнения 2а), 2б), 2в) и с учётом уравнения 3) имеем:
Fx(t)=Fx1+Fx2+Fx3=-Wb^2*Rb*M1*cos(Wb*t+270)-Wb^2*Rb*M2*cos(Wb*t+270)-Wb^2*Rb*M3*cos(Wb*t+270)=
=    Fx(t)=-Wb^2*Rb*(3*M)*cos(Wb*t+270)

С проекциями на ось У аналогично (с заменой "cos" на  "sin") и т.о:
 
"Трехточечный ротор" нужно рассматривать как одну точку с массой 3М=М1+М2+М3
вращающуюся вокруг оси b на расстоянии Rb с частотой Wb, и соответственно уравновешивать эту массу противовесом.
Т.е. сажаем на основной эксцентриковый вал "ротор", балансиры для уравновешивания "3М", а оборотов ротора Wa в конечной формуле нет. Как же так? 🙁 
Какая печалька для алхимиков дисбалансов из-за особых "разнооборотных сочетаний  магических положений ротор-вал"  ;D

может расчеты надо подкорректировать  😉

:STUPID

 

[martensito]

Чтобы не заморачиваться с рисованием векторов сил,  уравнения для проекций сил на оси Х и У.

Точки a=Ш, b=К, массы М1=М2=М3=М, их сумма = 3*М, массы "ротора жесткого трехточечного" вращаются вокруг оси а с частотой Wa (и r=Ra); сама ось а вращается вокруг оси b с частотой Wb (и r=Rb).

может расчеты надо подкорректировать  😉

а массы "ротора жесткого трехточечного" вращаются вокруг оси b или только вокруг оси а

 

[БортСтрелок-Радист...]

Господа Теоретики: а как\бы вернуться ближе к ТЕЛУ (мат\части), а именно - интересует Ваши ИМХУ в плане применения AIXRO XF40: надежность\ресурс\расход в горизонте-наборе\болячки & etc.-:question
Планирую установить в кач\ве СУ 1-мест. аэрошюта...

 

[Андрей Миллер]

Планирую установить в кач\ве СУ 1-мест. аэрошюта... 

Вот кто нам расскажет трясет РПД или нет! И если трясет, то как! 🙂

 

[БортСтрелок-Радист...]

Тока эксплуататоры могут: Ау-у... [smiley=smiley_up.gif]

 

[martensito]

It`s alive
https://youtu.be/jokKno29WLU

 

[TsAI]

It`s alive

кто "живой" то? гламурный кузов? тетка с бэйджиком? а где ж сам "живой" скайактив с зумзумом? Типа РПД...   как всегда - деревянный чурбак-макет под капотом... 

 

[martensito]

как всегда - деревянный чурбак-макет под капотом...  

 

[СУ]

была проведена модернизация моего роторного двигателя. 

Приветствую, коллега. Поздравляю с успешным решением интересной конструкторской задачи. Будем ждать продолжения вашего проекта.

Приветствую, коллега!
Что-то немного затихла ветка. Не хотелось бы думать, что и сюда проникло холодное веяние геополитических проблем.

Когда-то в мае этого года мы с Вами полемизировали относительно сравнения двигателей Ванкеля и Грэя-Школьника. Ещё тогда я намеревался сделать видео-ролик, где была бы показана прямая взаимосвязь между конструкциями их механизмов. Но получилось так, что его я сделал только совсем недавно, работая над оформлением новой главы своего сайта http://roto-motor.com/index.php?id=89 .
Приглашаю Вас посмотреть этот ролик - видео 11.

Кстати, было бы интересно узнать, как Ваши успехи в изготовлении образца двигателя Грэя-Школьника, которого Вы собирались делать?
 

 

[МаГент]

прямая взаимосвязь между конструкциями их механизмов...

интересно узнать, как Ваши успехи в изготовлении образца двигателя Грэя-Школьника, которого Вы собирались делать? 

Не быстро, но движемся последовательно... 😉 Сейчас делаем системы: зажигания, подачи топлива, смазки... Нечто вроде стенда. Фотки ротора, статора и крышки уже выкладывал. На форум заглядываю, но не каждый день... 😱
Ваша мысль об одинаковости механизмов сомнений не вызывает. Радует, что продолжаете свои поиски. Собственно мы об этом тогда же и говорили. При этом отмечали, что основное преимущество Грея перед Ванкелем в другом, в неподвижности узлов уплотнения.

 

[СУ]

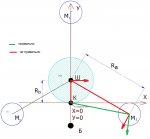
прямая взаимосвязь между конструкциями их механизмов...

интересно узнать, как Ваши успехи в изготовлении образца двигателя Грэя-Школьника, которого Вы собирались делать? 

Не быстро, но движемся последовательно... 😉 Сейчас делаем системы: зажигания, подачи топлива, смазки... Нечто вроде стенда. Фотки ротора, статора и крышки уже выкладывал. На форум заглядываю, но не каждый день... 😱
Ваша мысль об одинаковости механизмов сомнений не вызывает. Радует, что продолжаете свои поиски. Собственно мы об этом тогда же и говорили. При этом отмечали, что основное преимущество Грея перед Ванкелем в другом, в неподвижности узлов уплотнения.

Ну, если так, почему бы и нет. Но я лично, касательно места крепления уплотнений, до сих пор не вижу принципиально большой разницы с Ванкелем.
Точно так же, как в роторных секциях и Ванкеля, и Грэя, и в том числе в поршневой секции, эти радиальные уплотнения (на роторе - вместе с осевыми уплотнениями) играют ещё одну важную функцию - силового амортизатора, удерживая ротор в определённой зоне пространства рабочей полости, предотвращая ударное столкновение ротора (поршня) со стенками рабочей полости статора при его пространственном перемещении. Благодаря уплотнениям-амортизаторам, ротор получается как бы "вывешенным" в пространстве рабочей полости. Ведь если данные амортизаторы убрать из механизма, то, с учётом необходимости существования зазоров, ротор (поршень) при вращении вала тут же заклинится относительно стенок статора.
Кстати, в прошлый раз Вы, очевидно, не обратили внимания на мой вопрос о том, каким образом в двигателе Грэя происходит осевое уплотнение ротора? На сайте Школьника я почему-то не заметил присутствие таких осевых уплотнений на плоскостях ротора. Или может быть, и я об этом не знаю, они там и вовсе не нужны? А если они где-то там всё же есть, то они у Вас тоже будут укреплены на статоре, таким же образом, как и радиальные уплотнения?
Может быть, действительно, на том сайте я как-то невнимательно приглядывался к осевым уплотнениям? 

 

[Грей]

Благодаря уплотнениям-амортизаторам, ротор получается как бы "вывешенным" в пространстве рабочей полости. Ведь если данные амортизаторы убрать из механизма, то, с учётом необходимости существования зазоров, ротор (поршень) при вращении вала тут же заклинится относительно стенок статора.

А, что в РД Школьника  ротор не "вывешен" в пространстве рабочей полости радиальными уплотнениями?