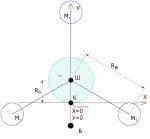
Чтобы не заморачиваться с рисованием векторов сил, уравнения для проекций сил на оси Х и У.
Точки a=Ш, b=К, массы М1=М2=М3=М, их сумма = 3*М, массы "ротора жесткого трехточечного" вращаются вокруг оси
а с частотой Wa (и r=Ra); сама ось
а вращается вокруг оси
b с частотой Wb (и r=Rb).
1) Найдем проекцию на ось Х равнодействующей F(t) сил (от движения масс с ускорением) приложенные к точке b :
Fx(t)=Fx1(t)+Fx2(t)+Fx3(t); (далее (t) опускаем для краткости, а рисунок берем за положение системы при t=0)
2) раскладываем ускорения движущихся масс (М1, М2, М3) и соотв. силы на составляющие (уравнения их проекций на Х):
2а) Fx1=Fax1+Fbx=-Wa^2*Ra*M1*cos(Wa*t+270)+(-)Wb^2*Rb*M1*cos(Wb*t+270);
2б) Fx2=Fax2+Fbx=-Wa^2*Ra*M2*cos(Wa*t+30)+(-)Wb^2*Rb*M2*cos(Wb*t+270);
2в) Fx3=Fax3+Fbx=-Wa^2*Ra*M3*cos(Wa*t+150)+(-)Wb^2*Rb*M3*cos(Wb*t+270).
3) Fаx=Fax1+Fax2+Fax3=
= -Wa^2*Ra*M1*cos(Wa*t+270)-Wa^2*Ra*M2*cos(Wa*t+30)-Wa^2*Ra*M3*cos(Wa*t+150)=
0 (т.к. ротор уравновешен вокруг своей оси
a).
4) складываем уравнения 2а), 2б), 2в) и с учётом уравнения 3) имеем:
Fx(t)=Fx1+Fx2+Fx3=-Wb^2*Rb*M1*cos(Wb*t+270)-Wb^2*Rb*M2*cos(Wb*t+270)-Wb^2*Rb*M3*cos(Wb*t+270)=
= Fx(t)=-Wb^2*Rb*(3*M)*cos(Wb*t+270)
С проекциями на ось У аналогично (с заменой "cos" на "sin") и т.о:
"Трехточечный ротор" нужно рассматривать как одну точку с массой 3М=М1+М2+М3
вращающуюся вокруг оси
b на расстоянии Rb с частотой Wb, и соответственно уравновешивать эту массу противовесом.
Т.е. сажаем на основной эксцентриковый вал "ротор", балансиры для уравновешивания "3М", а оборотов ротора
Wa в конечной формуле нет. Как же так?
🙁
Какая печалька для алхимиков дисбалансов из-за особых "разнооборотных сочетаний магических положений ротор-вал" ;D