вопрос по креплению крыла

[Lapshin]

...Перешли к подсчету количества ангелов на кончике иглы?
Не валяйте дурака:сделать точный расчет и распределить сечения,выгрызаякаждый лишний миллиграмм не удастся по-любому - хотя бы потому,что не сможете точно смоделировать нагрузки.
Так к чему же эта софистика и замыливание вполне ясных вещей?

 

[M.Gennadij]

Давайте не будем уходить в сторону

Я хочу понять, зачем меня пытаются заставить решать школьные задачки. Если коротко, то будет изгиб по двум осям (если рассматривать с точки зрения изгиба) или сжатие по диагонали (если рассматривать с точки зрения растяжения-сжатия), одно другому не противоречит.

 

[PFELIX]

Я хочу понять, зачем меня пытаются заставить решать школьные задачки

Так поймите, что при сжатии (только при сжатии) Ваш общий случай именно таков, что моменты именно равны, т. е. просто его (изгибающего момента) нет, и между двумя шарнирными узлами его в принципе быть не может. Само тело пытаются сжать, не очень красиво, но не более того.
И даже про неравные моменты говоря, еще раз акцентирую внимание, помните про отличие конструкции от механизма, откуда там моментам взяться.

 

[Михаил-Нск]

Теперь для полноты картины добавьте ещё одну "кочергу" и учтите что между собой кочерёжки соединены моментно.

Так поймите, что при сжатии (только при сжатии) Ваш общий случай именно таков, что моменты именно равны, т. е. просто его (изгибающего момента) нет, и между двумя шарнирными узлами его в принципе быть не может. Само тело пытаются сжать, не очень красиво, но не более того.

Попробую привести к логическому завершению спор о наличии момента в шарнирно опертой балке. В узлах крепления балки моментов нет (надеюсь, это сомнений не вызывает). Возьмем классический случай - один из узлов на оси жесткости (рис. 1). Эквивалентная расчетная схема представлена ниже. Распределение эпюр от сил сжатия и моментов в ответе №100. Такая картина доказана теоретически и практически многими научными мужАми. Спорить о том, как в действительности распределяются силы по сечения балки и где именно находится горизонтальная часть буквы "Г", особого смысла нет - абсолютно точно этого не знает никто. Для практики достаточно знать, что там есть момент и его можно сосчитать.
В обсуждаемом случае (рис. 2) вид эквивалентной расчетной схемы может быть таким, как представлено ниже, либо, как в первом случае, суть не меняется - момент присутствует и он в 2 раза больше, чем в первом случае.
Теперь все мы дружно об этом знаем. Пора уже обсуждать - как сделать так, чтобы негативное влияние этих моментов минимизировать (с учетом того, что на лонжерон воздействует еще целая куча нагрузок).

 

[PFELIX]

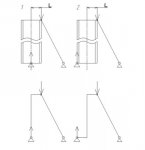
Для практики достаточно знать, что там есть момент и его можно сосчитать.

Вот это подвел. Ну и сосчитай. В каком, конкретно сечении балки какой момент.
Полагаю don migel в посту 107 вовсе не так собирался соединять кочерги, как у Вас на рисунке ниже.
Что же касается минимизации нагрузок с практической точки зрения, самым легким (в прямом смысле слова) решением является подпор стенок по консолям, какой-то кронштейн все-равно делать, и с нервюрой можно кницами стенку лонжерона соединить, а остальное ну просто смешная ловля блох, потому как есть понятие эксплуатационной прочности, что порой накладывает гораздо большие ограничения по уменьшению веса конструкции. Ну, типа упал случайно  гаечный ключ на оболочку крыла и пробил ее, а по спектру расчетных нагружений был двукратный запас прочности.
При этом еще необходимо сказать, что при нагружении как на рисунке в посту 36 нагрузки на полки лонжерона будут суммироваться и вычитаться даже облегчая рассматриваемые нагрузки в сравнении с идеализированной схемой, заставляя незагруженные части полок работать и, наоборот, разгружая местные напряжения. Сами нагрузки именно от изгибающих моментов, именно на балку лонжерона, а не на его полки, несравнимо больше, нежели нагрузки в местах распределения напряжений от неидеально выполненного кронштейна (узла и т.п.). А в месте крепления к фюзеляжу других (изгибающего момента, кручение не рассматриваем) и вовсе не будет.

 

[don migel]

Так поймите, что при сжатии (только при сжатии) Ваш общий случай именно таков, что моменты именно равны, т. е. просто его (изгибающего момента) нет, и между двумя шарнирными узлами его в принципе быть не может. Само тело пытаются сжать, не очень красиво, но не более того.

Ну вот в самую точку,моменты есть но они равны и компенсируют друг друга хотя и действуют относительно разных осей,если тело (лонжерон)имеет одинаковую жёсткость по двум осям то изгиба не будет, если жёсткость по одной из осей будет больше то будет S образный изгиб. Я имею в виду,что изгиб тела происходит не от наличия одного изгибающего момента,или преобладания одного момента над другим,моменты всегда одинаковы и противоположны.Изгиб происходит в силу действия моментов относительно разных осей и свойств тела по этим осям.

Полагаю don migel в посту 107 вовсе не так собирался соединять кочерги, как у Вас на рисунке ниже.

Подтверждаю,не так.

 

[Михаил-Нск]

Ну вот в самую точку,...Я имею в виду,что изгиб тела происходит не от наличия изгибающего момента...Изгиб происходит в силу действия моментов ...

Наличия момента нет, но действие есть!  ;D Короче - гнётся, потому что гнётся.
Лучше делать так, чтоб не гнулось (по крайней мере от сил реакции подкоса).

 

[don migel]

Ну вот в самую точку,...Я имею в виду,что изгиб тела происходит не от[highlight] наличия изгибающего момента[/highlight]...Изгиб происходит в силу действия моментов ...

Наличия момента нет, но действие есть!  ;D Короче - гнётся, потому что гнётся.
Лучше делать так, чтоб не гнулось (по крайней мере от сил реакции подкоса).

Извиняюсь, в этой фразе имел в виду  наличие одного изгибающего момента .Исправил.

 

[M.Gennadij]

Так поймите, что при сжатии (только при сжатии) Ваш общий случай именно таков, что моменты именно равны, т. е. просто его (изгибающего момента) нет, и между двумя шарнирными узлами его в принципе быть не может.

Так поймите, что в большинстве случаев решение любой физической задачи можно произвести несколькими способами и формальное решение этой задачи с помощью  моментов будет точно таким же, как и с помощью растяжения-сжатия. Следует заметить, что при решении в общем виде этой задачи с помощью моментов, с геометрией тела в виде параметров, приведённая конфигурация буде частным случаем. Если интересует только такой вид, то разумеется проще решать с помощью  растяжения-сжатия.

 

[M.Gennadij]

если тело (лонжерон)имеет одинаковую жёсткость по двум осям то изгиба не будет, если жёсткость по одной из осей будет больше то будет S образный изгиб. Я имею в виду,что изгиб тела происходит не от наличия одного изгибающего момента,или преобладания одного момента над другим,моменты всегда одинаковы и противоположны.Изгиб происходит в силу действия моментов относительно разных осей и свойств тела по этим осям. 

Я ожидал подобных высказываний (только не знал каких) Мягко говоря Ваше высказывание не соответствует действительности. Странно, что Вы не заметили рисунок в 118 ответе. Хотелось бы услышать объяснение с помощью Вашей "теории".

 

[M.Gennadij]

просто его (изгибающего момента) нет, и между двумя шарнирными узлами его в принципе быть не может. 

Я надеюсь, Вы сами поймёте что это бред. Если нет, то нарисую схему.

 

[M.Gennadij]

И даже про неравные моменты говоря, еще раз акцентирую внимание, помните про отличие конструкции от механизма, откуда там моментам взяться.

По подробнее пожалуйста. Вы полагаете, что в конструкции не может быть изгибающих моментов?

 

[don migel]

Странно, что Вы не заметили рисунок в 118 ответе. Хотелось бы услышать объяснение с помощью Вашей "теории".

Извиняюсь за моё колхозное образование,но я честно не понимаю какие узлы заделки на вашем рисунке и красные стрелки это две силы или проекция от другой силы?

 

[M.Gennadij]

какие узлы заделки на вашем рисунке

Шарнирная заделка по углам тела. 

красные стрелки это две силы или проекция от другой силы? 

Это две силы равные по значению, но противоположные по направлению, приложены по углам тела.

 

[don migel]

Тело изогнётся по вертикальной оси так ( зелёным).

 

[M.Gennadij]

Тело изогнётся по вертикальной оси так ( зелёным

То что изогнётся по вертикальной оси, это очевидно. Как быть с Вашим утверждением

Я имею в виду,что изгиб тела происходит не от наличия одного изгибающего момента,или преобладания одного момента над другим,моменты всегда одинаковы и противоположны.Изгиб происходит в силу действия моментов относительно разных осей и свойств тела по этим осям. 

При такой схеме, изгибающий момент по горизонтальной оси при любом соотношении сторон будет равен нулю.

 

[don migel]

Я вам в #119 сразу сказал что этот случай не наш у нас узлы заделки по другому и сила по диагонали.

То что изогнётся по вертикальной оси, это очевидно. Как быть с Вашим утверждением

Я имею в виду,что изгиб тела происходит не от наличия одного изгибающего момента,или преобладания одного момента над другим,моменты всегда одинаковы и противоположны.Изгиб происходит в силу действия моментов относительно разных осей и свойств тела по этим осям. 

При такой схеме, изгибающий момент по горизонтальной оси при любом соотношении сторон будет равен нулю. 

Это высказывание относится к моему рисунку(рассматриваемой схеме,диагональное закрепление,диагональное нагружение),а не к вашему..

Хотелось бы услышать объяснение с помощью Вашей "теории".

Я не претендовал на открытие" теории" ,я объяснил данный случай так как его понимаю я.

 

[PFELIX]

PFELIX писал(а) Вчера :: 07:24:19:
просто его (изгибающего момента) нет, и между двумя шарнирными узлами его в принципе быть не может. 

Я надеюсь, Вы сами поймёте что это бред. Если нет, то нарисую схему.

Очень бы хотелось посмотреть.

 

[M.Gennadij]

Очень бы хотелось посмотреть.

Любое тело, ось жёсткости которого не совпадает с прямой, проходящей через оси шарниров, будет иметь изгибающий момент. Из этого можно сделать вывод, что имея две пластины имеющие одинаковые размеры крепежных отверстий, толщину и площадь, но отличающиеся тем, что первая пластина имеет ось симметрии совпадающей с направлением силы, а вторая асимметрична, то при сжатии критические силы на первой пластине будут больше.

 

[M.Gennadij]

Это высказывание относится к моему рисунку(рассматриваемой схеме,диагональное закрепление,диагональное нагружение),а не к вашему..

Да, если тело имеет прямоугольную форму, если оси шарниров на диагонали на углах, и так далее, то изгибающие моменты по двум осям жёсткости равны. Не понятно, в чём практический смысл.