Бесшатунные двигатели - 2
- Статус
Господа! Вспомните, на какой ветке форума Вы находитесь...
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
Какая альтернативка? Господь с вами, милейший, всё из курса физики и математики за 10 класс.
Итак... продолжим урок.
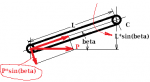
Р*sin(beta) -это тангециальноя составляющая силы Р. Отражает ту часть силы Р, которая создаёт момент отн. т.С
Вложения
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
Вы спросили про уравнения, где сумма моментов равна нулю. Я показал. как составил ТАКОЕ уравнение Баландин.
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
Во избежание разночтений я нарисовал. Повторение для нерадивого ученика - мать учения.
Момент на шатуне равен произведению тангециальной сотавляющей силы Р на плечо L.
Mc=F2*L
Вложения
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
Андрей. Вот уже больше двух недель Вы не можете написать простую формулу для момента на ПКВ, тот, под буковкой М от силы Р. Жду с нетерпением.
Вложения
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
Да помню про "БЕСШАТУННЫЕ ДВИГАТЕЛИ"!!
Дело в том, что С.Баландин расчитывал свои двигатели на основании разложения сил в КШМ. Но откуда-то у него взялся некий момент на ПКВ, про который у нас с Владимиром Александровичем завязалось небольшое обсуждение.
Так как Баландин смело поставил момент на ПКВ, я столь же смело поставил момент на шатуне, при этом указал, чему он равен, как в дальнейшем расклад с моментом приходит к классическому разложению силы Р на S и N., аргументируя это построениями.
Наличие или отсутствие этого момента связано с возникновнием боковой силы N и может уменьшить эту силу на два порядка в некоторых схемах БШМ. Поэтому разговор считаю достаточно важным для понимания сути преобразования движения в БШМ и его отличия от КШМ.
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
Не понятно. Картинку, пожалуйста, вы ж умеете.
Извините, но Вы какой-то дуростью занимаетесь- хотя я ведь на ветке типа "конструкторов" бесшатунников. :🙂
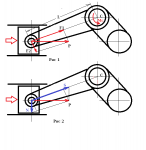
Из математики - любую равнодействующую силу на шатуне (по оси шатуна) можно разложить бесконечное число раз способами на любое количество осей - из ваших картинок следует что фантазии хватило только на два варианта. Один из них, рис.2, классический - для удобства определения-рисования силы давления на поршень т газов и силы от стенки цилиндра.
От каждой в отдельности разложенной силы (если она не по оси шатуна) будет какой-то момент - и что с того? - это даже круглому троечнику должно быть понятно.
Но интересна в итоге, для шатуна, результирующая сила.
А момента от РЕЗУЛЬТИРУЮЩЕЙ СИЛЫ на шатуне без учета трения в подшипниках головки (в статике или при" бесконечно медленном" вращении) НЕТ и быть не может - иначе не было бы по определению статической неподвижной картинки и никаких нарисованных раскладов сил - так как в динамике появляются совсем другие уравнения с учетом ускорений, моментов инерции, сил инерции и т.д. - это совсем запредельно для "бесшатунных умов". 🙂
В динамике и сложном движении с ускорением на шатуне появляется "собственный" изгибающий момент под действием распределенных сил инерции - расклад давал по ссылке JohnDoe (растет человек в знаниях) в своем посте пару страниц назад - но даже этого здешние "инженеры-
Это даже Миллер в своих секретных и "альтернативных" формулах расчета ДВС понять не смог. 🙂
Бредятина - начните с азов, а то заходишь на ветку совковых, да еще бесшатунных, инженеров... - "караул". Как-то силы на "трапецеидальных" поршневых кольцах неделю раскладывали и искали вожделенное уменьшение прижимной силы. 😱
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
В отличии от царицы математики за расклады в физике определяют РЕАЛЬНЫЕ СИЛЫ, поэтому предложено только ДВА варианта, причём из первого вылезает второй, то есть, по факту, один. А фантазии, да, мало не бывает.Edg сказал(а):
Edg сказал(а):
То есть эта схема КШМ тоже бред?
Вложения
Сосед Николаич
Все великие идеи проходят стадию мечты и бреда.
Патетика понятна, напор справедливого возмущения тоже. Не понятно, что за зверь "РЕЗУЛЬТИРУЮЩАЯ СИЛА на шатуне". Огромная просьба, нарисовать.
Это Вы в книге видите фигу(с)
Где Вы там момент на шатуне узрели от результирующей силы Fрезультирующая=P-N) ? - любую стрелку "крутящую" к шатуну как итоговый момент всех сил воображаете? - это не так, тот момент действует на блок цилиндра за счет боковой силы от поршня N на стенку цилиндра и вращает его, цилиндр (и "тянет" шатун за собой в динамике)
Все нарисовано на картинках - результирующая сила направлена вдоль оси (стержня) шатуна и соединяет оси вращения. Точнее сказать на картинках результирующая сила на верхней головке шатуна - точно такая же навстречу будет на нижней голове шатуна от кривошипа коленвала. Они друг друга уравновешивают и направлены по оси шатуна - отсюда момент любой из этих сил НОЛЬ относительно любой головки и оси вращения шатуна, и система (и шатун) уравновешены в статике - в динамику Вам лезть рано.i-gukov сказал(а):
И момент силы всегда приводит к изгибающим нагрузкам , хоть при вращении хоть без оного.
Сосед, мне уже надоели ваши фантазии и неумные попытки вывернуться из тупика, в который вы сами себя загнали.
Миллер вам задал вопрос:
Вместо того, чтобы честно признать свою ошибку, вы полезли изобретать очередной фантастический бред - взяли плечо L и пристроили к нему воображаемую силу.
Честно - утомили ваши постоянные изворачивания и безумные фантазии, на сим заканчиваю, ибо все это в данной теме флуд.
Рекомендую вам не замусоривать эту ветку, и если уж вам непременно требуется доказать правильность своих заблуждений - откройте новую тему для этого
Миллер вам задал вопрос:
Ваш ответ:
Теперь, когда я вас ткнул носом в вашу детскую ошибку, доказав, что согласно правилам механики, плечом силы Р (а не ее момента) относительно точки С длина шатуна L НЕ ЯВЛЯЕТСЯ, вы тут же начинаете вилять и пишите:
Вам не кажется, что в вашей формуле речь идет уже не про плечо силы Р (про которое вас спрашивали и вы ответили первоначально), а выдуманной вами силы F2?
Вместо того, чтобы честно признать свою ошибку, вы полезли изобретать очередной фантастический бред - взяли плечо L и пристроили к нему воображаемую силу.
Честно - утомили ваши постоянные изворачивания и безумные фантазии, на сим заканчиваю, ибо все это в данной теме флуд.
Рекомендую вам не замусоривать эту ветку, и если уж вам непременно требуется доказать правильность своих заблуждений - откройте новую тему для этого
Кстати, картинки в посте "Соседа" 10700 нарисованы неверно и "криво" - сила по оси шатуна должна быть равнодействующей от суммы сил давления (на поршень) и боковой реакции стенки (на поршень), которые в сумме передаются на головку шатуна.
То есть, N (или F2 как вариант разложеният) должна быть направлена в обратную сторону - в итоге эти две картинки будут
Все то у вас криво и неверно выходит даже в элементарных картинках, Сосед Николаевич?! 🙂
ПыСы
Картинки с разложением сил Соседа Н ВЕРНЫ - был неправ, погорячился - пардон. И чего это народ "не вомзутился"? 🙂
Ранее сказанное мною:
" сила по оси шатуна должна быть равнодействующей от суммы сил давления (на поршень) и боковой реакции стенки (на поршень), которые в сумме передаются на головку шатуна"
тоже верно и вытекает из классической картинки разложения Соседа Н.
Андрей Миллер
Я люблю строить самолеты!
- Откуда
- Санкт - Петербург
Если из математики Лобачевского, то может быть. Но есть математика классическая Евклида и по ней все и работают....
Инерция и трение не учитывались, не надо умничать, про Вас непохоже... 🙂
Есть же дураки - не делают тавровые шатуны! 🙂
И их фамилия не Миллер! :~~)
Миллер, Вы и в математике .... скорее как двутавр - любую систему сил (кроме при наличии пары противоположных на плече, являющихся моментом), физически можно всегда свести к одной равнодействующей - и наоборот, разложить одну равнодействующую на ПРОИЗВОЛЬНЫЕ по направлению две силы(для плоскости), коих бесчисленное множество вариантов- и это все по Евклиду, и это все про шатун.
Они не учитывались в статических картинках от "Соседа Н", который в них не разберется все. А реальный ДВС имеет вращающиеся и подвижные узлы и подвержен инерциальным нагрузкам при работе - это азбука и основы, которые следует знать даже инженеру-третьеразряднику. И я не виноват, что некоторые
http://aviaciaportal.ru/sily-inercii-vyzyvajushhie-izgib-shatuna/
Такие, включая даже исключенного Миллера, вообще зачастую плохо понимают, что делают. 🙂
А умные не делают двутавр в шатуне тогда, когда обороты в КШМ умеренные, и соответственно изгибающие нагрузки от инерции не существенны или не критичны.
Автора книги куда-то занесло или криво отредактировали в печать - оси поршня и шатуна и так не совпадают кроме как в ВМТ и НМТ.
"Несовпадение" осей поршня, даже например палец поршневой расположен не на оси поршня или ось цилиндра смотрит "мимо" оси КВ, ни к каким статическим моментам на шатуне не ведет.
Стат. момент на шатуне появится если оси отверстий головок шатуна лежат не на оси статического момента его поперечного сечения - называется внецентровое сжатие или растяжение - но так специально никто не делает. Исключение - шатуны с прицепными шатунами в звездах или V-образных например, где геометрия нижней головки ведущего шатуна "сложная" и возникает внецентровое сжатие-растяжение в этом месте.
ПыСы Именно "динамический" изгиб шатуна от сил инерции в ВМТ и НМТ равен "0", и как раз оси шатуна и поршня в этот момент совпадают - может этот случай динамического изгиба и имел ввиду автор в учебнике - но это именно изгиб от сил инерции при ускорении частей шатуна в движении, которые (силы инерции) в этих точках направлены все строго по оси шатуна на сжатие в НМТ или растяжение в ВМТ.
Я смотрю что всех у вас заносит то в одну, то в другую сторону, и лишь один вы движитесь по идеальной прямой ;D
"...Кроме напряжения от сжатия и растяжения в стержне шатуна возникают дополнительные напряжения изгиба, вызываемые внецентровым приложением сил в плоскости, нормальной к плоскости качания..." (шатуна).
Теперь понятнее стало?
Это уже несовпадение в плоскости качания шатуна.
Проще говоря силы пытаются гнуть шатун в двух плоскостях
- Статус
Similar threads
